量子多体問題における誤り抑制#
前節では、一般の量子回路中のノイズを抑制する手段として外挿法を説明しました。 ここでは、量子コンピュータの重要な応用先である、量子多体問題に焦点を当て、特に基底状態計算における誤り抑制手法を紹介します。
\(\newcommand{\ket}[1]{| #1 \rangle}\) \(\newcommand{\bra}[1]{\langle #1 |}\) \(\newcommand{\braket}[2]{\langle #1 | #2 \rangle}\)
そもそも基底状態とは#
興味のある量子多体系\(\mathcal{S}\)に対応する\(d\)次元のHilbert空間を\(\mathcal{H}=\mathbb{C}^{d}\)とします。 \(\mathcal{S}\)が外界から孤立しているとすると、時刻\(t\)における系の量子状態\(|\psi(t)\rangle\)は、以下のSchrödinger方程式に従います：
ここで、\(H(t)\)は時刻\(t\)におけるハミルトニアンです。外場などの影響がない場合には、のように時間に依存しないものと仮定できます。 以下ではかんたんのため、\(N\)量子ビット系の時間非依存な系のハミルトニアン\(H(t)=H\)を考えることにしましょう。 孤立系の時間発展はユニタリ演算子で記述されることから、ハミルトニアンは\(H=H^\dagger\)を満たすエルミート演算子です。 したがって、固有状態は実の固有値を持ちます。特に、固有値\(E_i\)をもつ\(i\)番目の固有状態\(|E_i\rangle\)は以下のような固有方程式を満たします。
ここで、\(E_0 \leq E_1 \leq \cdots \leq E_{d-1}\)のように並べた時、最も小さい固有値\(E_0\)に対応する状態\(|E_0\rangle\)を 基底状態 (Ground state) と呼びます。
基底状態の計算例 1 : Heisenbergハミルトニアン、\(N=2\)サイト#
import numpy as np
# パウリ行列
x = np.array([[0, 1], [1, 0]])
y = np.array([[0, -1j], [1j, 0]])
z = np.array([[1, 0], [0, -1]])
# ハミルトニアン H = X1 X2 + Y1 Y2 + Z1 Z2（2サイト）
ham = (np.kron(x, x) + np.kron(y, y) + np.kron(z, z)).real
# 固有値と基底状態を求める
eigvals, eigvecs = np.linalg.eigh(ham)
print("基底エネルギー:", eigvals[0])
print("基底ベクトル:", eigvecs[:, 0]) # numpyの仕様に注意, 確かに singlet状態
基底エネルギー: -3.0
基底ベクトル: [ 0. 0.70710678 -0.70710678 0. ]
基底状態の計算例 2 : Heisenbergハミルトニアン、\(N=6\)サイト#
次に、Heisenberg相互作用をする量子ビットが1次元的に繋がった系を考えることにします。 周期境界条件のもとで、ハミルトニアンは
のように与えられているものとしましょう。この場合、\(N\)が十分小さい場合には、依然として厳密対角化が実行できます。
import scipy
from scipy.sparse import kron, identity
def heisenberg_chain(L):
"""LサイトのHeisenbergハミルトニアンを構築"""
x = np.array([[0, 1], [1, 0]])
y = np.array([[0, -1j], [1j, 0]])
z = np.array([[1, 0], [0, -1]])
def kron_all(op_list):
res = op_list[0]
for op in op_list[1:]:
res = kron(res, op) # sparse matrixとして情報を保持
return res
dim = 2 ** L
H = np.zeros((dim, dim), dtype=np.complex128)
for i in range(L - 1):
for S in [x, y, z]:
ops = [identity(2)] * L
ops[i] = S
ops[i + 1] = S
H += kron_all(ops)
return H.real
# 10サイトハミルトニアンの構築と固有値計算
n_qubit = 10
hamiltonian = heisenberg_chain(n_qubit)
eigvals, eigvecs = scipy.sparse.linalg.eigsh(hamiltonian, k=1, which='SA') # 最小固有値を求める
gs_en = eigvals[0]
print(f"{n_qubit}サイト基底エネルギー:", gs_en)
gsvec = eigvecs[:,0]
print(f"{n_qubit}サイト基底状態:", gsvec)
10サイト基底エネルギー: -17.032140829131514
10サイト基底状態: [-2.46908680e-17 8.66674272e-18 2.24968344e-17 ... 4.43596087e-18
8.57633712e-18 2.37263182e-17]
基底状態計算における誤り抑制： 量子選択配置間相互作用法(QSCI)/サンプルベース量子対角化法(SQD)#
以前にみたように、量子回路ではノイズが発生してしまうため、量子回路で実現しようとした量子状態は、意図したものとは別物になってしまいます。 そのような場合には、エネルギーを測定したとしても、全く別の値が得られることがしばしばあります。
ノイズのある基底状態#
前節では各量子ビットにおけるデコヒーレンスの影響を考えましたが、ここではノイズを最も抽象化したモデルとして、大域的脱分局ノイズを考えます。 具体的に、その作用は、入力の量子状態\(\rho\)に対して
のように表されます。ここで、\(p\)はノイズ率です。第2項の\(I/2^N\)は完全混合状態なので、口語的には「確率\(p\)で入力状態を完全混合状態と入れ替えるノイズ」と説明できます。
p = 0.4
rho = (1-p) * np.outer(gsvec, gsvec.conj()) + p * (np.identity(2**n_qubit)/2**n_qubit)
gs_noisy = np.trace(rho @ hamiltonian).real
print("Exact energy:")
print(gs_en)
print("Noisy energy:")
print(gs_noisy)
Exact energy:
-17.032140829131514
Noisy energy:
-10.219284497478908
QSCIもしくはSQD#
上で見たように、ノイズの影響は物理量の評価に大きな影響を与えてしまいます。より精密に実行する方法はあるでしょうか？
ここで、(NISQデバイスで)物理量を評価する際には「(1)量子回路の実行 → (2)量子測定によるサンプリング → (3)古典的な事後処理」という工程を経ることに注目します。
従来の評価方法では、(3)古典的な事後処理にて行われるのは非常に単純な操作です。具体的には、平均・中央値をとる、といった操作が相当します。 サンプリングの結果と古典計算機を最大限に活用できないか、との問題意識のもとで生まれたのがQSCI/SQDです。
考え方としては以下のようなものになります：
量子化学や物性物理の問題の中には、基底状態に対応する状態ベクトルを\(|\psi\rangle = \sum_i c_i |i\rangle\)のようにZ基底で表現した際、一部の計算基底\(\mathcal{S}=\{b_i\}_{i=1}^{K \ll 2^N}\)に集中していることがある。
そのような\(\mathcal{S}\)を知っていれば、射影演算子\(P_{\mathcal{S}} = \sum_{b\in \mathcal{S}} |b\rangle \langle b |\)によって、縮小されたハミルトニアン\(H_{\mathcal{S}} = P_{\mathcal{S}} H P_{\mathcal{S}}\)を作る。これを古典コンピュータで解けば良い。
実際には、\(\mathcal{S}\)そのものはわからないが、\(|\psi \rangle\)を近似的に知っている状況が現実的である。その場合、\(|\psi\rangle\)に対して射影測定を繰り返し、測定結果によって構成した\(\tilde{\mathcal{S}}\)を用いて、上の手順を実行すれば良い。
上の手順を図で表したのが以下です。詳しくは この論文を参照してください。
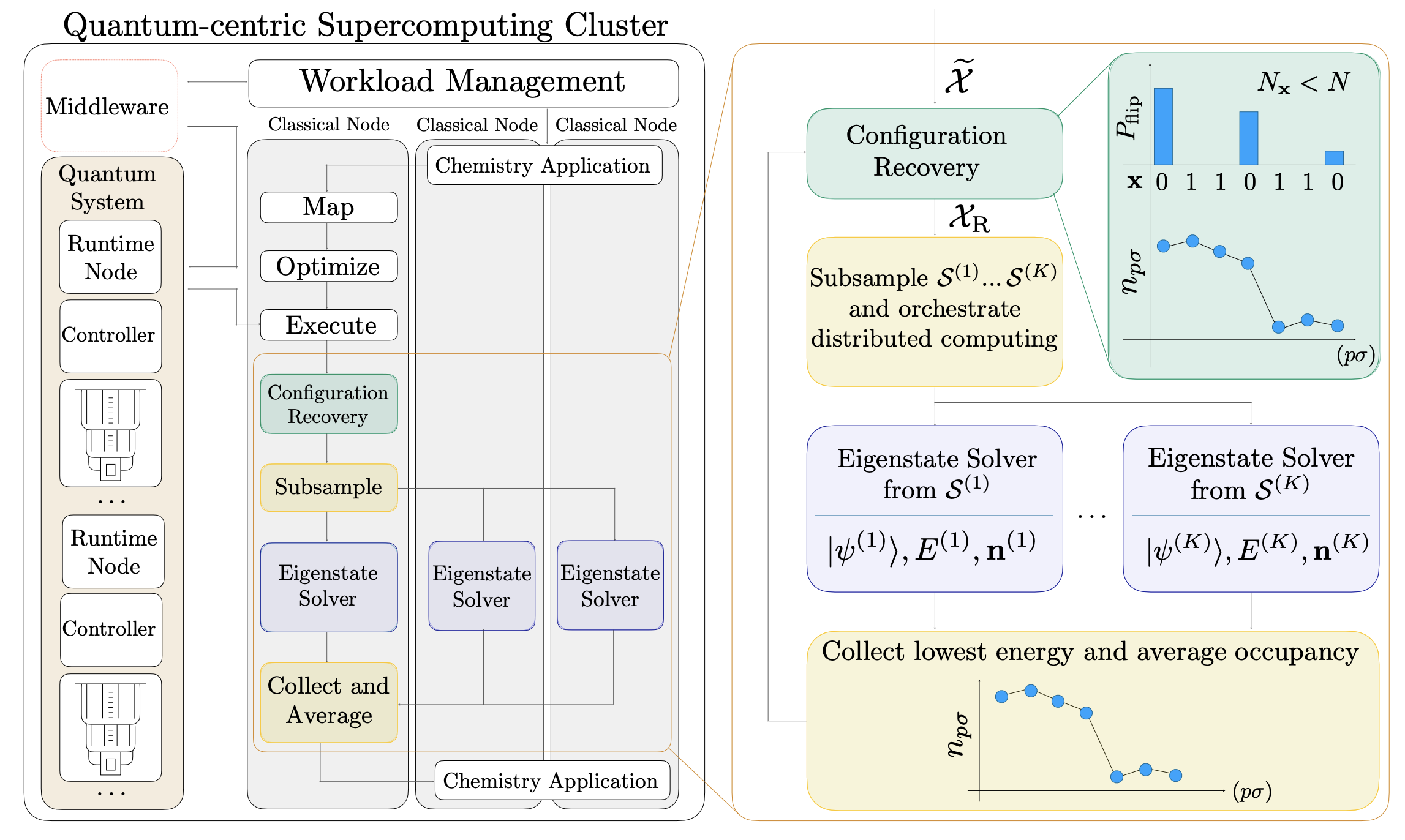
さて、QSCI/SQDの手法は、大域的脱分局ノイズのもとでは特に強力です。 なぜなら、ノイズのない理想的なサンプリングのもとでのQSCI/SQDは、ノイズのあるQSCI/SQDによって再現できてしまうからです。 大域的脱分局ノイズは「一定確率\(p\)で完全にシグナルを失う」ので、逆に\(1/(1-p)\)倍の回数だけサンプリングを実行すれば、元のシグナルと等価なものが得られると期待できます。 以下ではこれを確認しましょう。
[課題] 例えばパウリ演算子\(Z_1\)の期待値は大域的脱分局ノイズのもとでどのように振る舞うか？
[課題(難)] 大域的脱分局ノイズのもと、期待値を推定するためのサンプリングの回数は\(1/(1-p)^2\)倍されるが、これはなぜか。
(ヒント) 射影測定を1度実行した時の推定値が \(\{\pm 1\}\)であることに着目すると、期待値のestimatorは、該当の量子ビットで 0/1を測定した割合\(\hat{p}_{0/1} = N_{0/1} / (N_0+N_1)\)を用いて \(\hat{Z} = \hat{p}_0 \cdot 1 + \hat{p}_1 \cdot (-1)\)と書ける。サンプリングが理想的に実行できる場合、\(\hat{p}_0\), \(\hat{p}_1\)は真値\(p_0, p_1\)の周りで揺らいでいるが、大数の法則に従って精密なものになっていく。
probs_ideal = (np.abs(gsvec)**2).real
probs_noisy = rho.diagonal().real
n_sample = 200
states_sampled = np.random.choice(len(probs_noisy), size = n_sample, p = probs_noisy)
unique_bases = np.unique(states_sampled)
H_sub = hamiltonian[:, unique_bases][unique_bases, :] # 部分行列を抽出
energy_sub = np.linalg.eigvalsh(H_sub)[0]
print("reconstructed energy :")
print(energy_sub)
print()
print("Noisy energy:")
print(gs_noisy)
print("Exact energy:")
print(gs_en)
reconstructed energy :
-15.438686001501857
Noisy energy:
-10.219284497478908
Exact energy:
-17.032140829131514
ノイズのある量子回路における期待値を素朴に測定した結果と比べて、はるかに精度の良い結果が得られました。 測定回数を増やすと、構成された部分空間の次元は単調に増えていくことから、計算結果は系統的に改善されることが期待されます。
nsamp_array =[20,40, 80, 100, 150, 200, 300, 500, 800, 1000, ]
energy_noisy_array = []
energy_ideal_array = []
np.random.seed(123456) #再現性のためseedを固定
for n_sample in nsamp_array:
#ノイズのあるQSCI
states_sampled = np.random.choice(len(probs_noisy), size = n_sample, p = probs_noisy)
unique_bases = np.unique(states_sampled)
H_sub = hamiltonian[:, unique_bases][unique_bases, :] # 部分行列を抽出
energy_sub = np.linalg.eigvalsh(H_sub)[0]
energy_noisy_array.append(energy_sub)
# ノイズのないQSCI
states_sampled = np.random.choice(len(probs_ideal), size = n_sample, p = probs_ideal)
unique_bases = np.unique(states_sampled)
H_sub = hamiltonian[:, unique_bases][unique_bases, :] # 部分行列を抽出
energy_sub = np.linalg.eigvalsh(H_sub)[0]
energy_ideal_array.append(energy_sub)
import matplotlib.pyplot as plt
%matplotlib inline
plt.subplot(1,2,1)
plt.plot(nsamp_array, energy_noisy_array, "-o",label = "noisy QSCI")
plt.plot(nsamp_array, energy_ideal_array, "-o",label = "ideal QSCI")
plt.hlines(y = gs_noisy, xmin = min(nsamp_array), xmax = max(nsamp_array), linestyle = "--", color = "gray", label = "raw noisy")
plt.hlines(y=gs_en, xmin = min(nsamp_array), xmax = max(nsamp_array), linestyle = "-", color = "red", label = "exact")
plt.xlabel("# of samples")
plt.ylabel("energy")
plt.legend()
plt.subplot(1,2,2)
plt.plot(nsamp_array, np.abs(np.array(energy_noisy_array) - gs_en), "-o",label = "noisy QSCI")
plt.plot(nsamp_array, np.abs(np.array(energy_ideal_array) - gs_en), "-o",label = "ideal QSCI")
#plt.hlines(y = gs_noisy, xmin = min(nsamp_array), xmax = max(nsamp_array), linestyle = "--", color = "gray", label = "raw noisy")
#plt.hlines(y=gs_en, xmin = min(nsamp_array), xmax = max(nsamp_array), linestyle = "-", color = "red", label = "exact")
plt.xlabel("# of samples")
plt.ylabel("energy")
plt.yscale("log")
plt.legend()
<matplotlib.legend.Legend at 0x7f323321ed10>
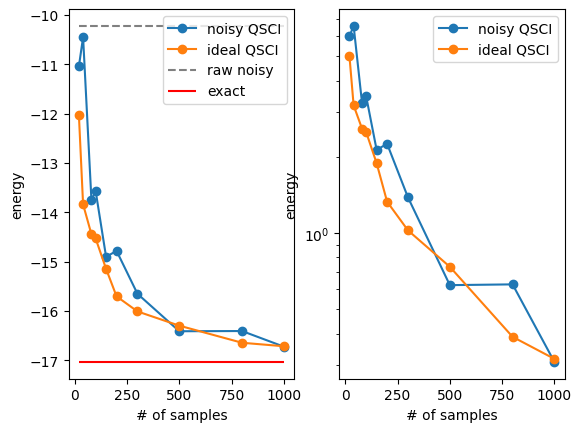
\(p=0.4\)ととっていたので、おおよそ\(1/(1-p) \approx 1.6\)倍程度のoverheadによってideal QSCIの計算結果を復元できています。